使用 Matplotlib 绘图
前言
Matplotlib 在 Python 中提供了类似于 MATLAB 的绘图支持,有人说使用 Numpy、Pandas、Scipy、Matplotlib 就可以完全替代 MATLAB。其中,Matplotlib 提供图像库支持,而 Numpy 提供优秀的向量计算、Pandas 提供便携的结构存储、Scipy 提供额外的计算库支持。Matplotlib 经常被用于数据分析,常常和 Numpy 等一起使用,本文不会系统的介绍这些库,而是从一些示例的方式快速入手 Matplotlib。
在阅读本文方面的建议是,你无需记忆每个模块,需要时将本文中的代码粘贴到你的 IDE 中然后尝试运行并根据你的需求改写。另外,提前声明作者本人并未使用过 MATLAB 而直接学习使用的 Matplotlib。
多样式平面折线
Matplotlib 绘图最常用的就是 matplotlib.pyplot.plot 方法,它接受主参数 、,表示对应的 坐标和 坐标,例如 表示第一个坐标点。另外,plot 提供一些辅参数,用于描述坐标点样式或坐标点连接样式。
1 | import numpy as np |
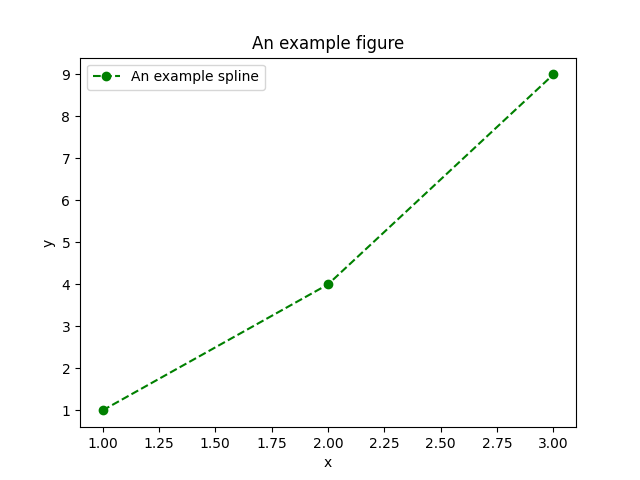
下面是全部样式展示。
1 | import numpy as np |
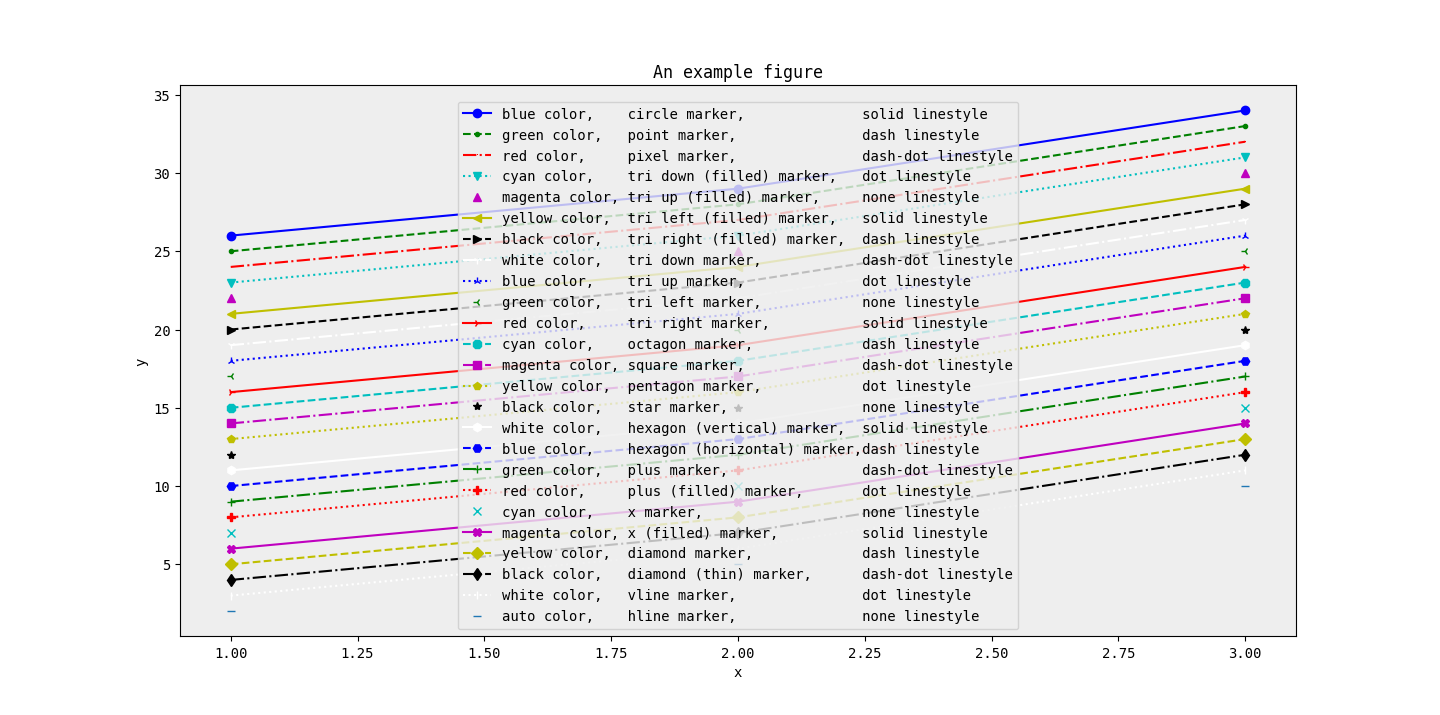
最后,matplotlib.pyplot.plot 的文档写的十分详细:
1 | import matplotlib.pyplot as plt |
绘制一元函数曲线
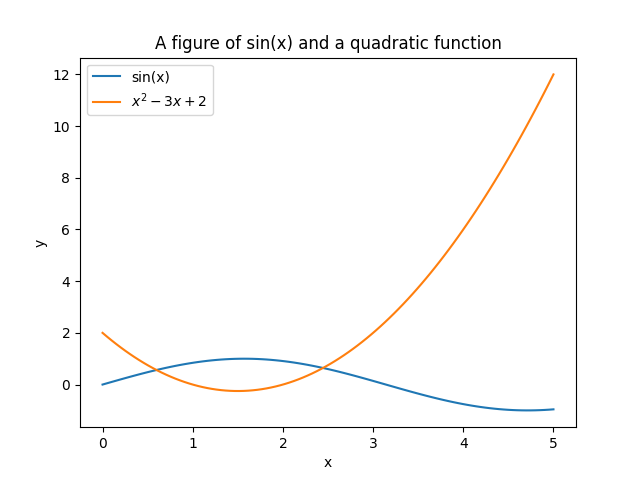
也许初学者会感到和认知有些出入,Matplotlib 只能通过传入样点绘制图像,那么如何绘制函数图像呢?其实很简单,样点足够多它就(看起来像)是一条曲线了。样点一般取 100 个即可。当然样点必须处理好后传入 Matplotlib 库,这里我们简单的用到了一些 Numpy 的内容。
1 | import numpy as np |
单图多表的绘制
也许你需要在一个页面中同时显示多个图表,这个问题当然也可以解决。我们将使用 matplotlib.pyplot.subplots 解决这个问题。
在使用 subplots 中也有几点需要注意:
-
subplots传入两个参数nrows/ncols,当其中一个参数为1时,其返回的axes是一维对象。1
2
3
4
5
6
7
8
9
10
11
12_, axes = plt.subplots(3, 1) # 创建 3x1 的子图表系
axes[2] # 索引 2 行 0 列的子图表
# axes[2][0] # 错误地, axes 是一维对象
_, axes = plt.subplots(1, 3) # 创建 1x3 的子图表系
axes[2] # 索引 0 行 2 列的子图表
# axes[0][2] # 错误地, axes 是一维对象
_, axes = plt.subplots(3, 2) # 创建 3x1 的子图表系
axes[2][0] # 正确地, axes 是二维对象
# 很奇怪? 我也觉得很奇怪... -
axes对象的常用方法集有plot/set_xlabel/set_ylabel/set_title/legend;而plt的常用方法集有plot/xlabel/ylabel/title/legend,注意区分。
下面是一个示例。
1 | from math import pi |
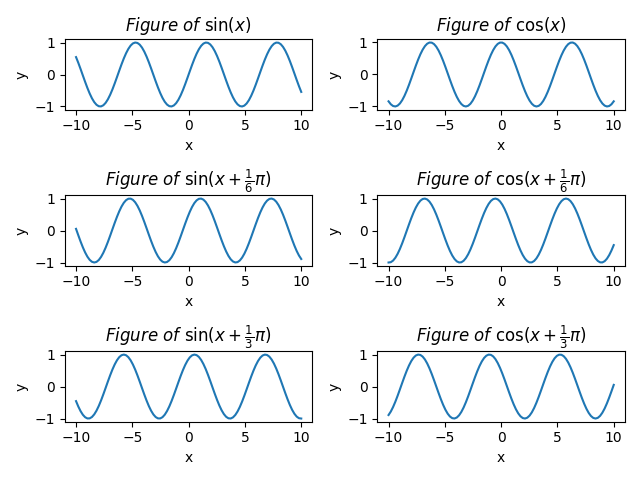
双纵坐标的绘制
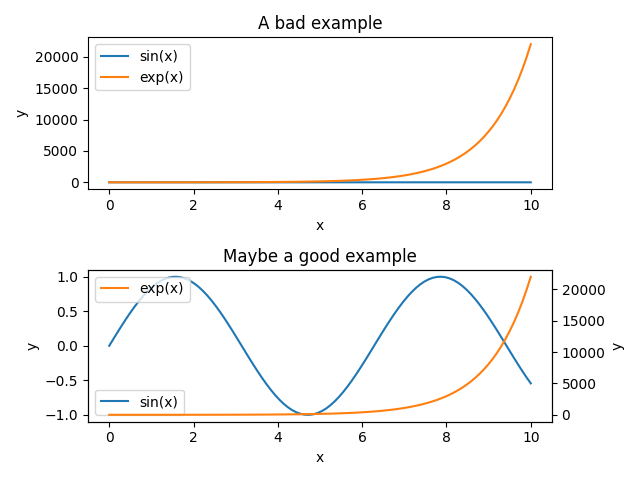
有时两个函数具有不同单位,或者两者是数量级的差距时,使用常规的坐标系无法呈现好的效果。下面提供我们将绘制一个双纵坐标,并与不使用双纵坐标对比。
1 | import numpy as np |
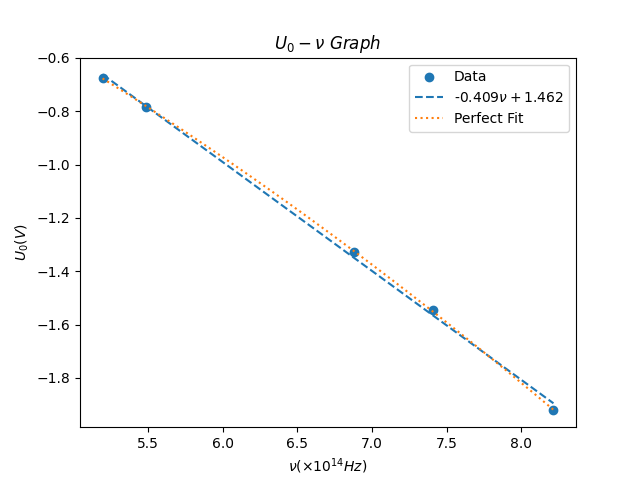
离散点函数拟合
在实验时,我们经常需要将离散点拟合成函数。例如,在我的物理实验课程中,就被要求绘制关系图像。当然实验并不要求使用计算机绘制图像,但有强迫症的我真的很难受。
- 线性拟合
- 完美拟合(高阶多项式)
1 | import numpy as np |
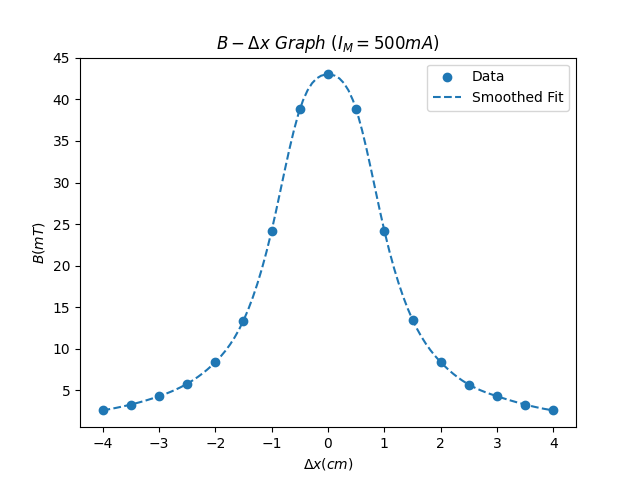
- 平滑拟合(数据插值)
1 | import numpy as np |
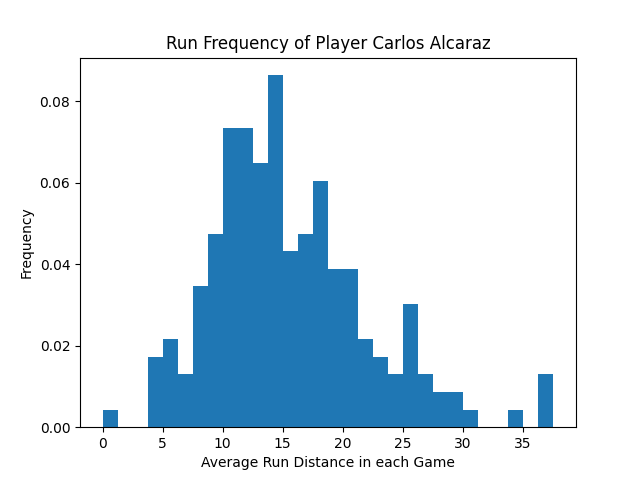
绘制频率直方图
频率直方图用于以柱状图的形式描绘样本中不同值出现的频率等信息。这里我们可以使用 matplotlib.pyplot.hist 直接绘制频率直方图,也可以使用 numpy.histogram 得到频率统计数据然后做进一步处理。
matplotlib.pyplot.hist绘制直方图
1 | import numpy as np |
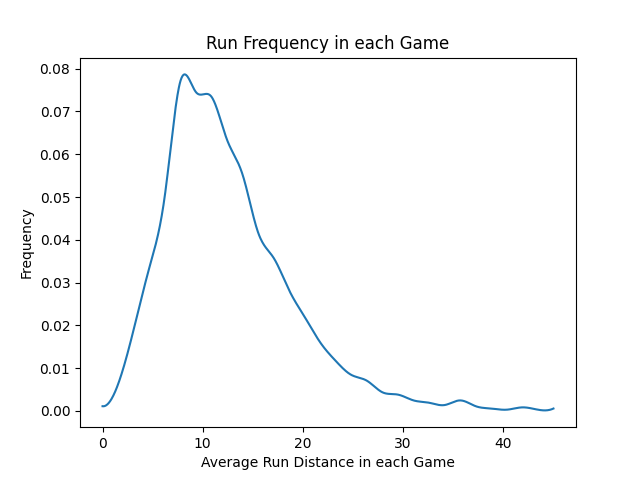
numpy.histogram绘制频率曲线
1 | import numpy as np |
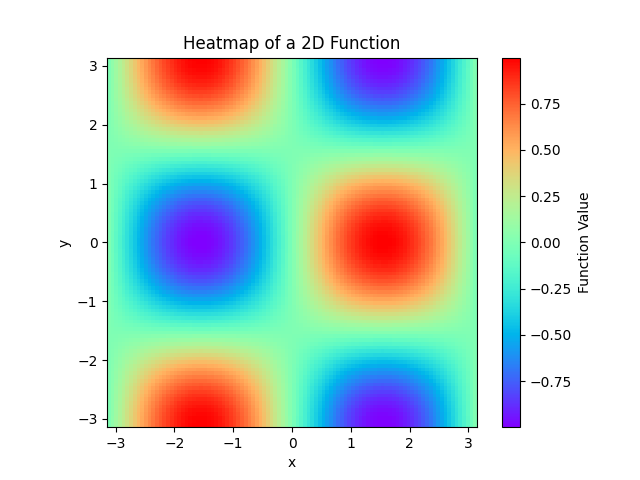
绘制二元函数热力图
绘制二元函数时,使用热力图是很常用的方法。它很多时候比三维图更加直观,当然我们后面也会介绍三维图的绘制。在二元函数绘制时,我们可能需要使用 Numpy 广播机制,另外将使用的 matplotlib.pyplot.imshow 接口比较特殊,它自动生成等差二元样点,而我们只需在 extend 参数传入 与 的上下界即可。
1 | from math import pi |
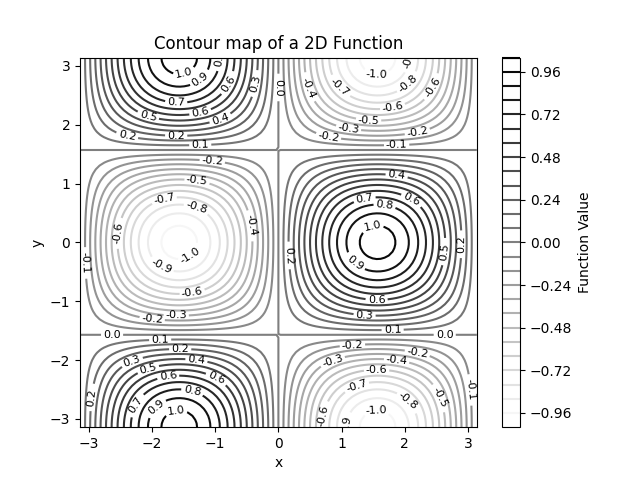
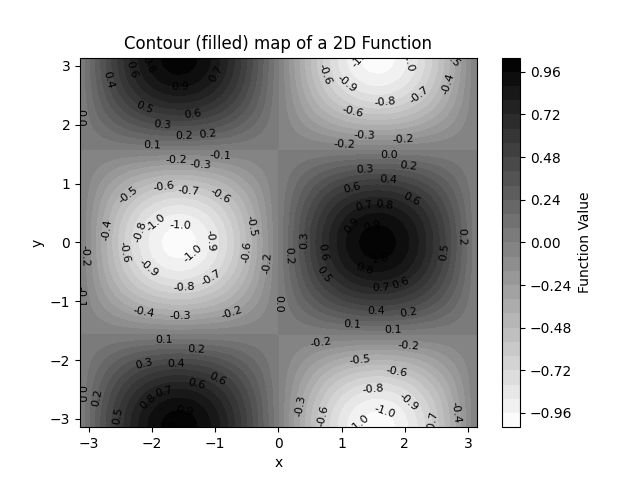
绘制二元函数等高图
绘制等高图与热力图功能和用法相似,并且它们使用了相同的 cmap 颜色样式。另外,我们还可以通过 contour 换成 contourf 得到另一种填充样式的登高图,这展示在我们最后的两张图像的对比中。
1 | from math import pi |
三维图表绘制
我个人并不推荐使用 Matplotlib 绘制三维图表,一是其导出的二维图片无法展现全部信息,二是其绘制的三维曲面效果一般。如果想要绘制二元函数,建议使用上面的介绍的 绘制二元函数热力图 / 绘制二元函数登高图。当然在可交互的情况下,Matplotlib 也可以展示直观的三维效果。
- 三维曲线绘制
1 | import numpy as np |
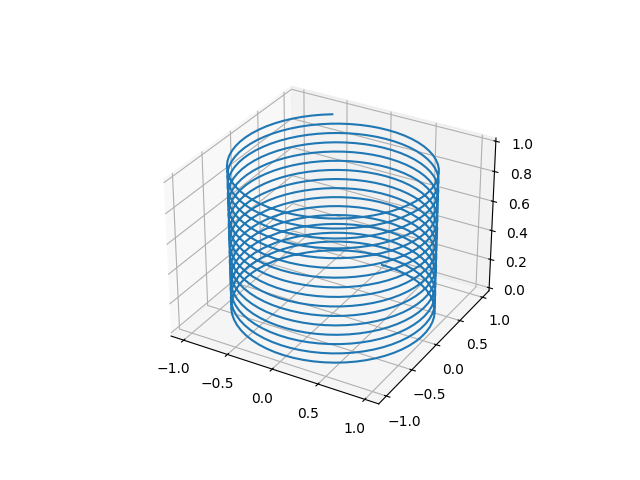
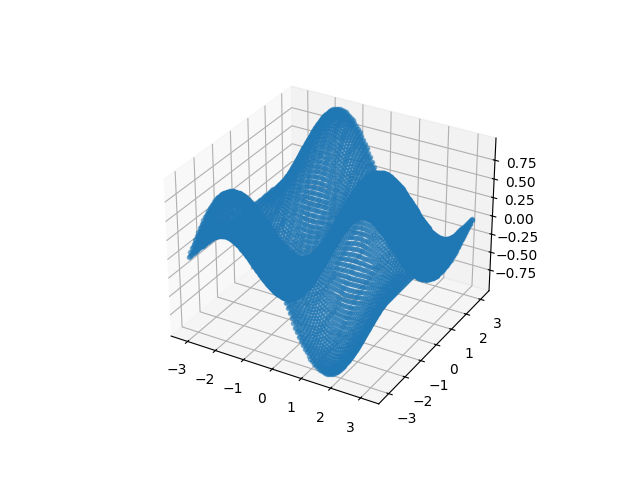
- 三维曲面绘制
1 | from math import pi |
动图绘制
- 二维动图绘制
1 | import numpy as np |
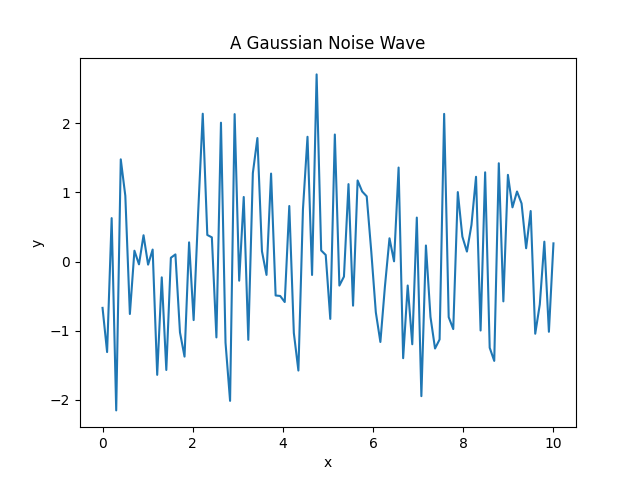
- 三维动画绘制
1 | from math import pi |
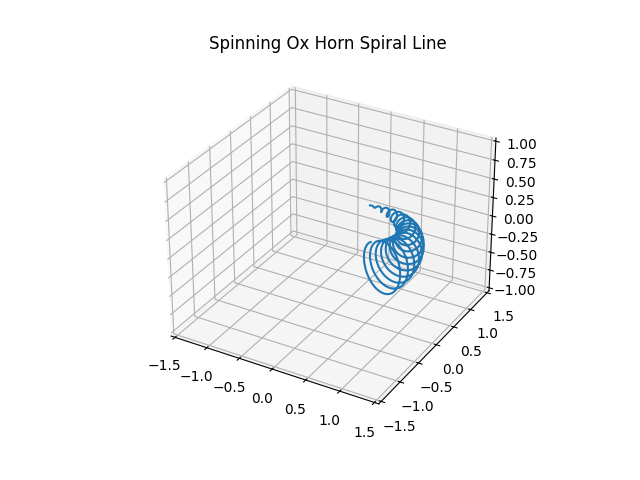
尝试使用上面的方法,构造并绘制一个稳定的三体运动(出自科幻小说《三体》)。
中文显示问题
这个问题其实只要设置中文字体即可。
1 | import numpy as np |
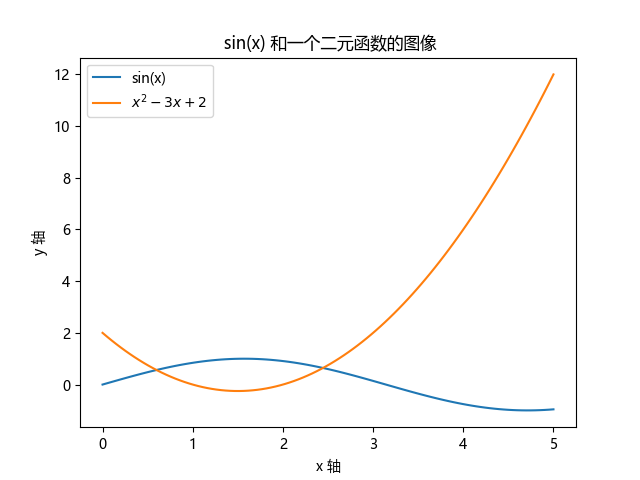
你可以使用下面的命令查看系统支持的字体。
1 | import matplotlib.font_manager |
