浅析几种一致性哈希算法

引入：什么是一致性哈希？

分布式集群与负载均衡

一个服务，例如一个网站为了方便管理通常由两部分组成：web 服务和对象存储服务。web 服务直接与用户建立连接，并且对用户请求进行解析、逻辑处理与响应。但是 web 服务通常是无状态的（可能会有一些缓存），这时就需要对象存储服务用来保存用户数据等信息。因此我们首先假设我们的架构由 web 服务（websvr）和对象存储服务（osssvr）两层组成。

当业务增长，服务的使用数量上升，这时就需要将 web 服务和对象存储服务拆分到两台机器上；当业务继续增长 ，一台 web 服务器和一台存储服务器无法继续承受业务压力，这时就需要构建 ​分布式集群 。

对于 web 服务来说这个过程很简单，由于 web 服务是无状态的，因此任何 web 服务可以处理任何用户的请求。但对象存储不同，不同的数据需要被路由到正确的位置。例如 userid = 100 的用户第一次接入到 websvr1，websvr1 随意（例如就近）将该用户的一个操作信息（例如注册）存储到了 osssvr1；第二天该用户接入到了 websvr4，于是 websvr4 路由到 osssvr4 发现用户未注册。

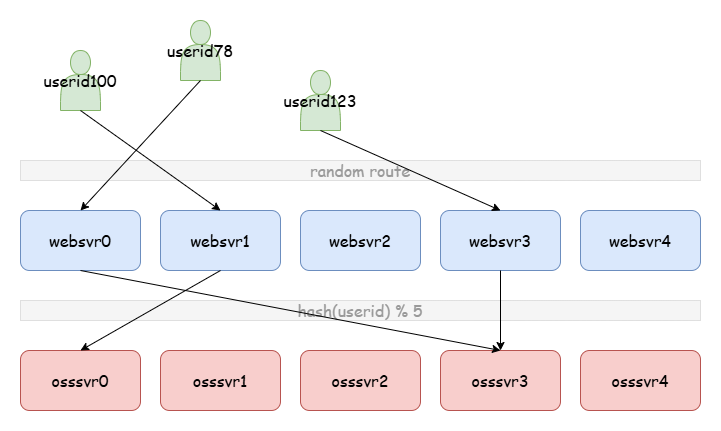
一种解决方案是增加一台机器提供元数据存储服务（metasvr），websvr 在新增数据时会将存储位置写到 metasvr 的路由表中，这样之后的所有数据都可以到 metasvr 路由。但这种做法存在两个问题：metasvr 存储的数据要足够少，否则它将成为新的存储瓶颈；metasvr 进行的响应要足够少，否则它将成为新的性能瓶颈。显然这两个条件它都不满足，这里我们先放一放。

另一种解决方案是对用户查询的键进行哈希作为路由。如 hash(userid) % 5 = 0，这样不管是哪台 websvr 接入用户请求，数据都会被路由到 osssvr0。这更像是一个协议，保证所有 websvr 将相同数据被路由到相同位置。到这里我们提出了 ​哈希 的概念。

分布式存储需要具备的第二个条件是 ​负载均衡 。这个问题我们发现轻松解决了，只要这个哈希算法够好，并且数据总量足够多，就能做到 osssvr 的负载均衡。

目标与挑战：扩容与缩容

嗯，问题当然没有这么简单，这个时候我们遇上了新的问题：集群需要动态的进行扩容和缩容来应对业务变化，我们如何来解决这个问题？

首先第一个问题是，能否重新实现 ​负载均衡 。一致性哈希算法和哈希算法一样，它要求能在数据存储时实现均衡，同时在扩缩容场景下，它也要求一致性哈希算法在进行数据迁移后仍然满足负载均衡。

一致性哈希算法通过数据迁移重新实现负载均衡，这个过程中 ​数据迁移量 是一个很重要的指标。理想最小迁移量的定义是，原有 n 台机器实现数据存储的负载均衡，如果扩容一台新的机器，每台机器的数据迁移量是 $\frac{1}{n+1}$，这样每台机器存储的数据量都变成原来的 $\frac{n}{n+1}$。

我们回顾一下前面 hash(key) % n 的哈希算法，它是一个好的负载均衡的算法，但可以发现并不是一个好的一致性哈希算法。假设原有 $hash(\text{key}) \% n = k$，则扩容后 $hash(\text{key}) \% (n+1) \ne k$ 的期望是 $\frac{n}{n+1}$，远高于最小迁移量的目标 $\frac{1}{n+1}$。你可以发现这其中主要迁移都花费在了原有机器间的数据迁移。

在一致性哈希算法的 “最小迁移量” 目标下，出现了新的挑战 ​一致性 。一致性是指在完成数据迁移后，所有机器都能保证正确路由到原数据的位置。就这一点 hash(key) % n 是一种一致性的哈希算法，你可以发现只要 websvr 知道机器的总数就总能路由到正确的数据位置。举例一个 “不一致” 的方案。前面讲到普通哈希方法数据迁移量主要浪费在了原有机器间的数据迁移，因此我们想到一个方案，如果数据迁移发生在原有机器间就不进行迁移，只有到新机器上的才进行迁移。但是也很容易发现这并不是一种满足一致性的方案。

我们可以发现，实现 ​负载均衡 和满足算法 ​一致性 ，是一致性哈希算法的基本要求，这两点必须做到。而减小 ​数据迁移量 ，则是评价一致性哈希算法好坏的主要标准。这样看来 hash(key) % n 也算是一种非常差的一致性哈希算法。

最后，还需要一提的是，一致性哈希算法总是需要一些元数据。还是拿 hash(key) % n 为例，起码在集群变更时，websvr 至少需要被告知 n 变成了 n+1，于是前面提到的 metasvr 就必不可少，但是它只能在扩缩容或故障等场景被调用；另外，例如前面提到的 “不一致” 方案，如果可以借助一些元数据实现一致也是可行的。我们后面将介绍的一些一致性哈希算法都需要一些元数据，其中一些数据结构还会复杂些，但这都在容忍的范围内。理论上只要元数据是基于机器，而非基于数据行的，元数据的大小都是可以容忍的。

Ring Hash

哈希环（Ring Hash）是最原始和经典的一致性哈希算法，其改版也很多。如：

• Karger（Consistent Hashing and Random Trees:
  Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web* 第 4 Consistent Hash 章节）、
• Rendezvous（A Name-Based Mapping Scheme for Rendezvous (umich.edu) 第 4 Mappings Based on Object Names 章节）、
• Dynamo（Dynamo: Amazon’s Highly Available Key-value Store）等，

其中 Karger 是第一次提出一致性哈希算法。

Ring Hash 的路由与扩缩容

哈希环是一种类似环状的数据结构，上面包含一些节点，每个节点表示一台机器。假设 key 通过哈希函数映射在 [0, 2^32) 的值域中。节点在初始化时会产生随机值，并将该节点放在环上的值位置，例如图中生成了 0 / 1006632960 / 2147483648 / 3221225472 四个节点。当 key 产生时通过 hash(key) 进行路由，并找到环上顺时针方向离它最近的节点作为宿主节点，例如图中 hash(key)=1.3e+09 路由到了机器 2147483648。

当进行扩容时，例如图中加入新的机器初始化随机值为 1476395008。可以发现 hash(key)=1.3e+09 的数据的顺时针最近节点发生改变，而 hash(key)=1.7e+09 的宿主节点没有发生改变。因此 hash(key)=1.3e+09 的数据应该进行迁移，准确的说 $hash(key) \in \left[1006632960,~1476395008\right)$ 的数据都应该进行迁移。

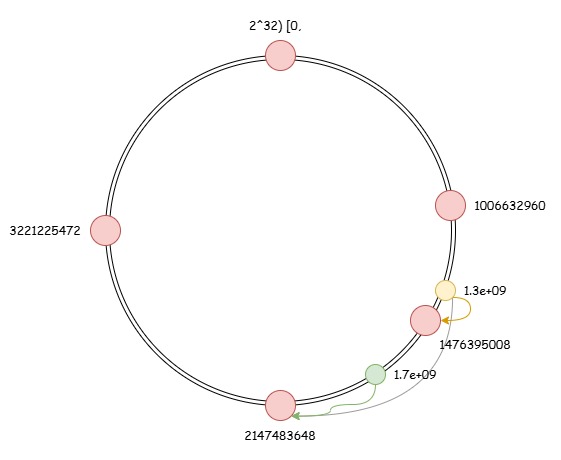
引入虚拟节点实现负载均衡

这里我们发现存在两个问题：

• 当新机器加入哈希环时，可以发现所有数据迁移发生在两台机器之间。例如图中所有数据迁移发生在 2147483648 到 1476395008 之间。这时扩容时负载全部集中在 2147483648。
• 机器的初始化随机值是随机的，通常没有特殊算法控制。这时事实上在机器数少时不容易实现好的负载均衡。例如图中机器 3221225472 占有大约 1/4 的数据，而 1476395008 仅持有约 1/8 的数据。

因此哈希环总是加入 ​虚拟节点 的概念，一台机器拥有几百上千个虚拟节点，这样即使只有两三台机器，也可以实现好的负载均衡。同时扩容时负载也能进行好的均衡。另外，每台机器拥有的资源可能是不同的，也可以通过调节虚拟节点之间的比值调节权重。

由于节点数量膨胀，数据在路由时可以使用二分查找快速找到宿主虚拟节点。

Jump Consistent Hash

Jump Consistent Hash 是 Google 于 2014 年提出的一种极简、快速的一致性哈希算法。其优势在于代码极其精简、不占用任何额外空间。原论文可参考：A Fast, Minimal Memory, Consistent Hash Algorithm (arxiv.org)。

Jump Consistent Hash 的代码极短，其核心代码只有短短几行：

int32_t JumpConsistentHash(uint64_t key, int32_t num_buckets) {
    int64_t b = 1, j = 0;
    while (j < num_buckets) {
        b = j;
        key = key * 2862933555777941757ULL + 1;
        j = (b + 1) * (double(1LL << 31) / double((key >> 33) + 1));
    }
    return b;
}

代码分层解释

直接看这段代码有些抽象，下面先分层解释一下：

令：

$$\begin{array}{l} hash(key) = 2862933555777941757 \cdot key + 1 \pmod{2^{64}} \\ prob(key) = \lfloor\frac{\lfloor\frac{hash(key)}{2^{33}}\rfloor + 1}{2^{31}}\rfloor \approx 2^{-64} \cdot hash(key) + 2^{-31} \\ \end{array}$$

则代码等价：

def Hash(key: int) -> int:
    # 这是一个好的散列函数, 可以假设每次返回随机值
    return (key * 2862933555777941757 + 1) % 2 ** 64

def Prob(key: int) -> float:
    # 尾部加数用于防止返回 0, 返回值域 (0, 1]
    return key * 2 ** -64 + 2 ** -31

def JumpConsistentHash(key: int, num: int) -> b:
    b, j = 1, 0
    while j < num:
        b = j
        key = Hash(key)
        j = (b + 1) / Prob(key)
    return b

可以看到这里的哈希函数 Hash 通过不断迭代，每次返回不同的散列值，可以认为是随机的。另外由于散列值值域为 $\left[0,~2^{64}\right)$，可得 Prob 的值域为 $\left(0,~1\right]$（这里的 Prob 看着会超过 1，但回头对比一下原代码是不会的）。这两个限定对后面负载均衡的证明很重要。

通过上面的代码可以看出 JumpConsistentHash 就是 j 指针的跳跃。将宿主机按 $\left[0,~num\right)$ 编号，当 j 指针第一次跳出 num 范围时，就取上一次未跳出时的编号（即 b）作为宿主机。这就是 JumpConsistentHash 的大致原理。

负载均衡证明

我们先来分析该算法的 ​负载均衡 性质，即证明从所有节点跳出的概率是相同的。

首先再次明确 $\text{Hash}(key)$ 可以认为是随机的，$Prob(key) \in \left(0,~1\right]$。

假设指针原位置为 b 则跳到 b+1 的概率为 $\text{Prob}(key) \in \left(\frac{b+1}{b+2},~1\right]$，跳到 b+2 的概率为 $\text{Prob}(key) \in \left(\frac{b+1}{b+3},~\frac{b+1}{b+2}\right]$，依此类推… 最后跳出并返回 b 的概率为 $\text{Prob}(key) \in \left(0,~\frac{b+1}{n}\right]$。由此，令 $p(b,~j)$ 表示从 b 跳到 j 的概率，则有：

$$p(b,~j)=\left\{\begin{array}{l} 0 & ,0 \le j \le b \\ (b+1)\left(\frac{1}{j}-\frac{1}{j+1}\right) & ,b<j<n \\ \frac{b+1}{n} & ,j = n \\ \end{array}\right.$$

令 $p(j)$ 表示经过若干次跳跃到 j 的概率，则有：

$$p(j) = \left\{\begin{array}{l} 1 & ,j=0 \\ \sum_{b=0}^{j-1}{p(b) \cdot p(b,~j)} & ,0 < j < n \\ \end{array}\right.$$

归纳、递推可得（自己归纳一下）：

$$p(j)=\frac{1}{j+1}~~~~,0 \le j < n$$

因此最终任意节点 j 作为宿主节点的期望 $q(j)$ 即为经过若干次跳跃到节点 j 并立即跳出范围，则有：

$$q(j) = p(j) \cdot p(j,~n) = \frac{1}{n}~~~~,0 \le j \le n$$

由此该算法理论上是负载均衡的。

一致性讨论

该算法显然是满足 ​一致性 的，Jump Consistent Hash 算法不需要任何数据，只需保证机器总数在集群各节点始终达成共识，那么 JumpConsistentHash 的返回值总是不变的。换言之，JumpConsistentHash 作为一个无状态函数，只要参数 key 和 num 不变其返回值就是不变的。

数据迁移量讨论

最后再来讨论一下 ​数据迁移量 问题：

当集群拥有 $n$ 个节点时，我们可以将从任意节点 $b$ 跳出编号范围的 $key$ 分为两类。第一类是 $n \le j < n+m$，这些节点在扩容 $m$ 个节点后将迁移到新机器；第二类是 $j \ge n+m$，它们仍然保留在原宿主机上。其中 $n \le j < n+m$ 的概率为 $\text{Prob}(key) \in \left(\frac{b+1}{n+m},~\frac{b+1}{n}\right]$，$j \ge n+m$ 的概率为 $\text{Prob}(key) \in \left(0,~\frac{b+1}{n+m}\right]$。可以发现对于任意节点 $b$ 的迁移量占比为 $\frac{m}{n+m}$，满足最小迁移量。

由此该算法理论上满足最小迁移量。

时间复杂度分析

可以发现到达每个点的概率的和就是经过点的个数的期望和。

$$T = \sum_{j=0}^{n-1}p(j) = \ln{n}+C \tag{C 是常数}$$

因此该算法的平均时间复杂度是 $\Theta(\ln{n})$。

Jump Consistent Hash 的缺陷

当然 Jump Consistent Hash 也有其缺陷，它的所有节点都必须连续编号。这在常规的扩缩容中没有问题，但是当有中间节点出现故障时 Jump Consistent Hash 无法进行有效的容错，因此这种一致性哈希算法通常需要其他的容错支持。

Maglev Hash

Maglev Hash 又是一种新颖的一致性哈希算法，它基于表查询，是 Google 在 2016 年发表的。原论文可参考：Maglev: A Fast and Reliable Software Network Load Balancer (storage.googleapis.com) 第 3.4 Consistent Hashing 章节。

建表和查询

首先 Maglev Hash 算法需要具有两个参数：M（散列空间，即哈希函数值域，必须是质数如 65537 / 655373）、N（节点或虚拟节点数）、Hash1 和 Hash2（两个独立无关的哈希函数）。其中 M 的值是固定不变的，N 会根据扩缩容变化。

Maglev Hash 在初始化时首先生成一张空表，然后进行填充序列。

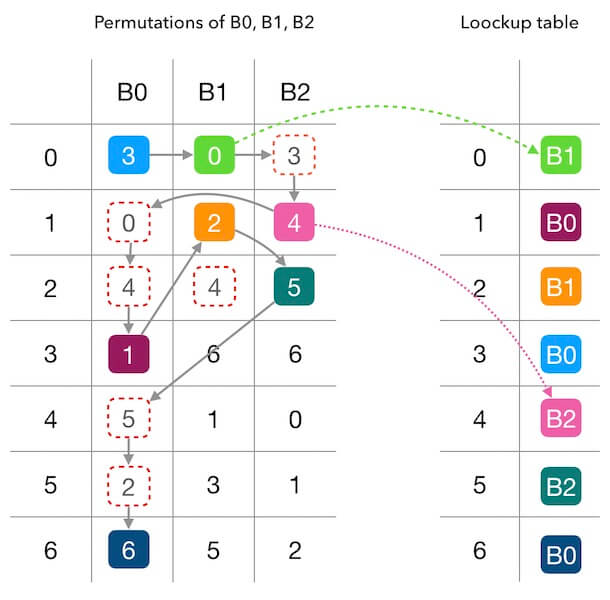
图中行标 0~6 表示哈希函数的值域空间，列标 B0~B2 表示节点编号。表中每一列是一个排列，各列独立无关。设列号为 $i$，行号为 $j$，表的生成是这样的：

$$\begin{array}{rl} offset[i] = & Hash1(i) \mod M \\ skip[i] = & Hash2(i) \mod (M-1) + 1 \\ table[j][i] = & \left( offset[i] + j \cdot skip[i] \right) \mod M \end{array}$$

由裴蜀定理，生成的每一列一定是一个排列。

得到排列表后，然后建查找表，我们直接来模拟一下这个示例即可。每个节点持有一个头指针，然后轮流向前走并添加到查找表中：

1. 从 B0 开始，拿到 $table[0][0]$ 里是 3，因此填 $entry[3]$ 为 B0；
2. 轮到 B1，从 $table$ 拿到 0，因此填 $entry[0]$ 为 B1；
3. 轮到 B2，拿到 $table[0][2]$ 里是 3，但是 $entry[3]$ 已经被占了；继续向下找，拿到 $table[1][2]$ 里的 4 没有被占用。
4. 重新轮到 B0，从之前的位置继续向下拿，依次拿到 0、4 都被占用了，直到拿到 1 并将 $entry[1]$ 标记为 B0。
5. 轮到 B1，从之前的位置继续向下拿，填 $entry[2]$ 为 B1。
6. …

有时候代码可能更直观：

int table[M][N];
int head[N];
int entry[M];

void BuildEntry() {
    // `table` has been filled
    for (int i = 0; i < N; i++) head[i] = 0;
    for (int j = 0; j < M; j++) entry[j] = -1;
    int i = 0, n = 0;
    while (n < N) {
        while (true) {
            int m = table[head[i]++][i];
            if (entry[m] == -1) {
                entry[m] = i;
                break;
            }
        }
        if (++i >= N) i = 0;
        n++;
    }
}

查询表建好了，那后面的查找过程也相当方便了。$key$ 的宿主节点就是 $entry[\text{Hash}(key)\%M]$，可以发现 Maglev Hash 最大的特色就是路由很快，是 $\Theta(1)$ 的。这里的 Hash 函数和前面的 Hash1 和 Hash2 都没有关系，可以是其中一个或者都不是都可以。

从这个建表过程，我们可以发现 Maglev Hash 具有 ​绝对良好的负载均衡 。因为 Maglev Hash 的负载均衡是依赖建表的，而前面介绍的其他一致性哈希算法都是依赖概率进行负载均衡的。

扩容和缩容

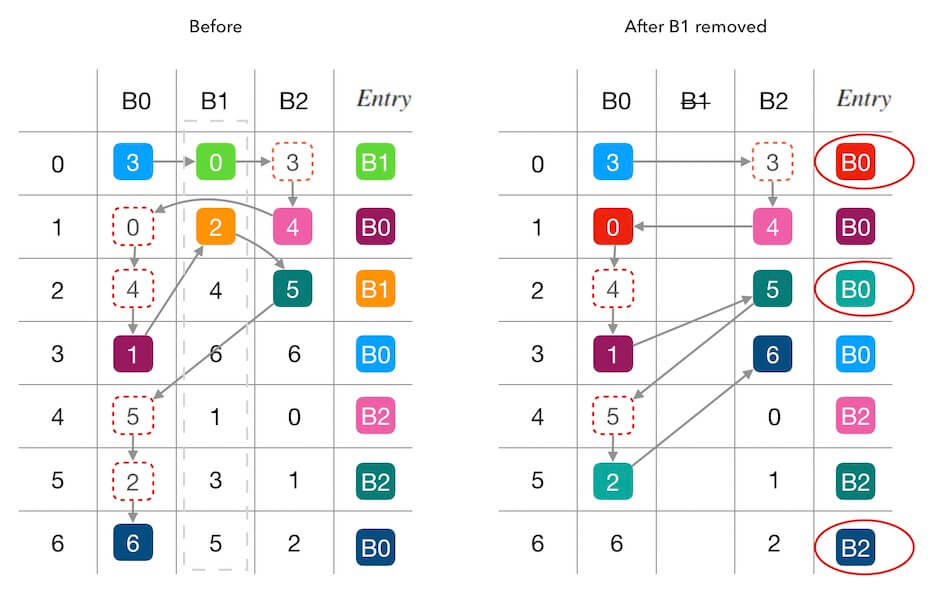
扩缩容的过程也很好理解，就是移除或者加入新的列后重新建查询表，之后就使用新的查询表即可。如上下图分别是缩容和扩容的示例。

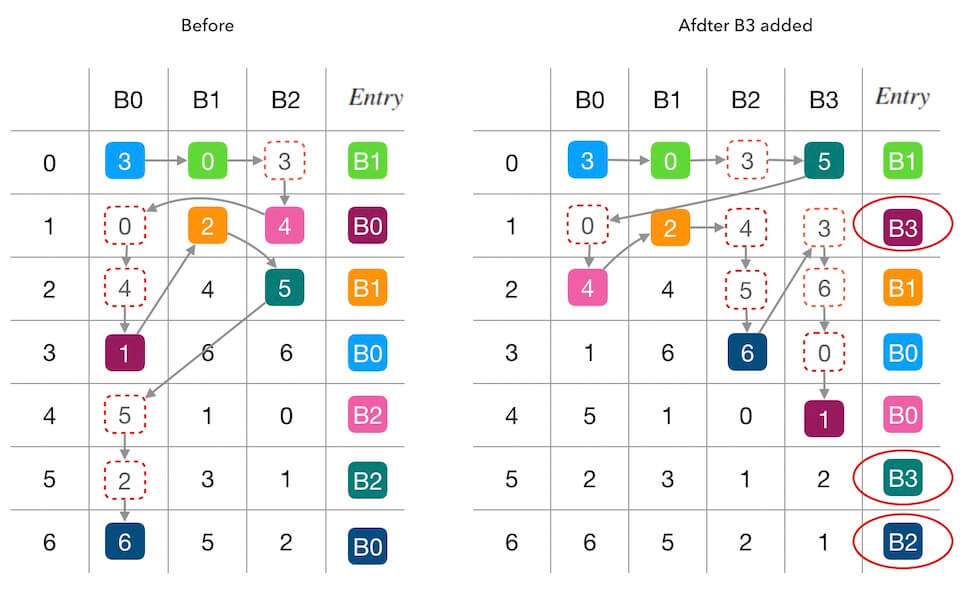
从图中我们也可以看出一个问题，Maglev Hash 并 ​不保证最小数据迁移量 。你可以发现在缩容的示例中，移除 B1 但是出现了 B0 到 B2 的数据迁移。在扩容的示例中也出现了 B0 到 B2 的数据迁移。

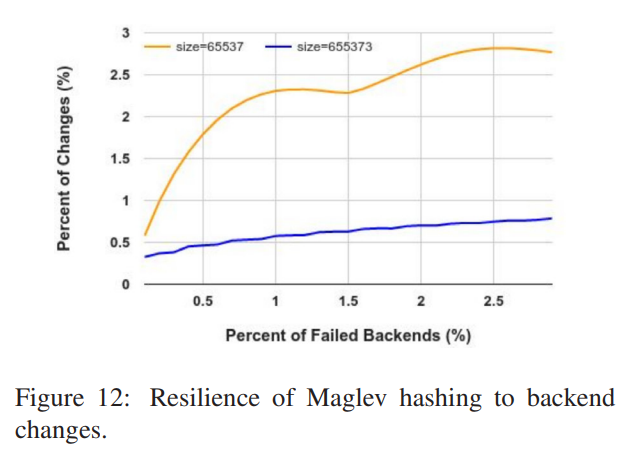
论文没有证明冗余数据迁移发生的期望，但通过实践数据展示了当 $M=655373$ 时该扰动基本可以控制在 $1\%$ 以下。

建表时间复杂度分析

前面讲到 Maglev Hash 的查询复杂度是 $\Theta(1)$ 的，现在我们来讨论它的建表复杂度。

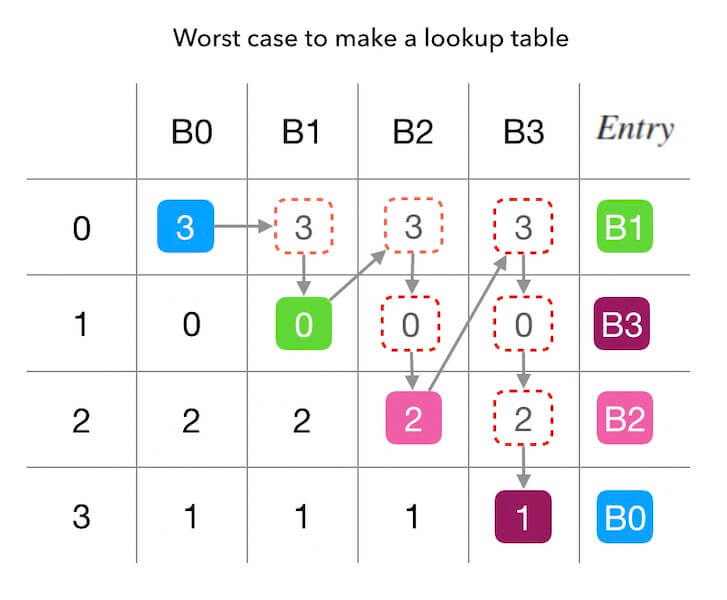
首先 ​最坏时间复杂度 是 $\Theta(NM)$ 的。因为最坏情况下所有节点生成相同的排列，这样遍历的表格数约为 $\frac{NM}{2}$。

然后来分析 ​平均时间复杂度 。注意到第一次一定能一次成功，$e(0)=1$；第二次有 $\frac{1}{M}$ 的概率和第一次的值碰撞，碰撞期望次数为 $e(1)=\frac{M}{M-1}$ 次；第三次有 $\frac{2}{M}$ 的概率与前几次碰撞，碰撞期望次数为 $e(2)=\frac{M}{M-2}$ …；第 $(n+1)$ 次有 $\frac{n}{M}$ 的概率与前几次碰撞，碰撞期望次数为 $e(n)=\frac{M}{M-n}$（独立重复试验）。由此可得总期望次数：

$$E = \sum_{i=0}^{n-1}{e(i)} = M(\frac{1}{M}+\frac{1}{M-1}+\frac{1}{M-2}+\dots+1) \approx M(\ln{M}+C)~~~~\tag{C 是常数}$$

由此平均时间复杂度为 $\Theta(M\ln{M})$。

对比几种一致性哈希算法

	Ring Hash	Jump Consistent Hash	Maglev Hash
一致性	所有一致性哈希算法必须满足	所有一致性哈希算法必须满足	所有一致性哈希算法必须满足
负载均衡	一般，添加虚拟节点实现较好的负载均衡	良好，通过概率控制的良好负载均衡	绝对好，建表分配实现绝对的负载均衡
数据迁移量	最小迁移量	最小迁移量	存在扰动，实践证明 M=655373 时扰动约为 1%
迁移负载均衡	一般，添加虚拟节点实现较好的迁移负载均衡	良好，通过概率控制的良好迁移负载均衡	一般，不满足最小迁移量
查询时间复杂度	$\Theta(N)$ / $\Theta(\log{N})$	$\Theta(\ln{N})$	$\Theta(1)$
变更时间复杂度	$\Theta(NV)$	$\Theta(1)$	$\Theta(M\ln{M})$
空间复杂度	$\Theta(NV)$	$\Theta(1)$	$\Theta(MN)$ / $\Theta(M\ln{M})$
容灾	可以支持	不支持随机删除，需要额外支持	可以支持

（其中 $N$ 为机器节点数；$V$ 为每个节点的平均虚拟节点数，Ring Hash 必须有虚拟节点，其他算法默认没有；$M$ 为散列空间，只有 Maglev Hash 依赖散列空间大小）

Reference

Blogs

什么是一致性哈希? - 小林coding

一致性哈希算法(合集) - 春水煎茶 · 王超的个人博客

Papers

Consistent Hashing and Random Trees: Distributed Caching Protocols for Relieving Hot Spots on the World Wide Web*

A Name-Based Mapping Scheme for Rendezvous (umich.edu)

Dynamo: Amazon’s Highly Available Key-value Store

A Fast, Minimal Memory, Consistent Hash Algorithm (arxiv.org)

Maglev: A Fast and Reliable Software Network Load Balancer (storage.googleapis.com)