布隆过滤器及其误判率推导

前言

本文将首先介绍布隆过滤器 (Bloom Filter) 是如何工作的，然后我们将形式化推导布隆过滤器的误判率。布隆过滤器是一种使用多哈希的方式判断元素是否属于集合的数据结构，他的优势在于不需要存储任何键值，非常节约空间且高效。

布隆过滤器被广泛应用于分布式或非分布式的存储系统中，用于快速判断数据是否位于对应的磁盘块中，从而减少穿库（访问不存在所需数据的磁盘块），如 LSM Tree 可能存在的无效磁盘访问。正因为布隆过滤器非常节约空间，它可以在有限的内存空间概括大量的磁盘信息。

在开始之前假设你了解哈希表。

工作原理

插入数据

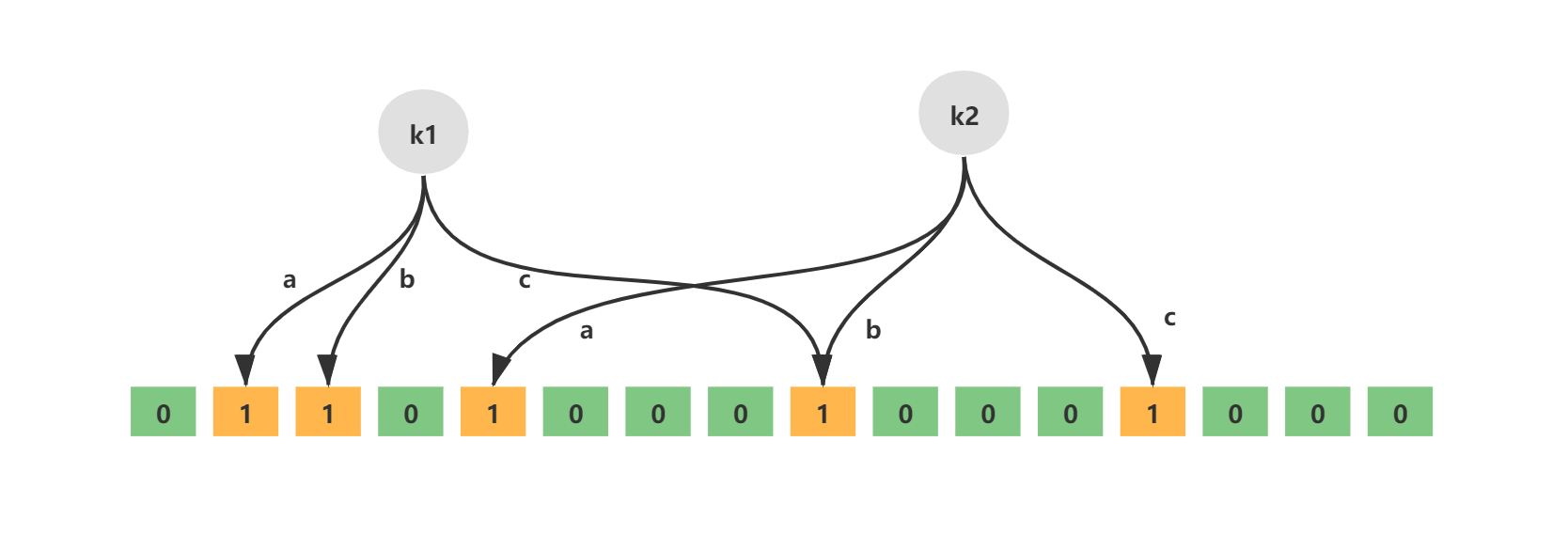
对于上面这个示例，我们需要将两个键 k1、k2 放入布隆过滤器中。如图布隆过滤器是一个相当简单的数据结构，它仅由一个位数组构成，图中每个方格实际占用一个比特位，这就是为什么说布隆过滤器非常省空间。

布隆过滤器具有两个参数：n 和 k。其中 n 表示过滤器占用的比特位的数量，例如这个示例中 n=15；而 k 表示对于每个需要插入的键，具有 k 个不同的哈希函数，例如这个示例中 k=3。如果布隆计数器具有 k 个哈希函数，那它进行一次插入、查找的时间复杂度为 $O(k)$。

现在需要插入 k1 和 k2，我们分别对它们执行 k 个哈希函数，假设我们得到：

$$\begin{array}{l} (hash_a(k1)~\%~n,~hash_b(k1)~\%~n,~hash_c(k1)~\%~n)=(1,~2,~8) \\ (hash_a(k2)~\%~n,~hash_b(k2)~\%~n,~hash_c(k2)~\%~n)=(4,~8,~12) \\ \end{array}$$

这时我们需要将它们对应的位进行置位，k1 会将第 $(1,~2,~8)$ 位置为 $1$，k2 会将第 $(4,~8,~12)$ 位置为 $1$。这样我们就标记了 k1 和 k2 的存在，得到了如图将 $(1,~2,~4,~8,~12)$ 标记的结果。需要注意的是，我们实际没有将键值存储，因此我们无法避免误判，这是出于空间的考量。

查找数据

现在假设我们需要判断新的数据是否存在，首先我们需要通过相同的方法计算哈希序列，这里有三种可能：

• $hash_{abc}(k1)=(1,~2,~8)$，这些位被置位，我们认为 $k1$ 存在于布隆过滤器。实际上 $k1$ 确实存在于过滤器。
• $hash_{abc}(k3)=(1,~2,~8)$，这些位被置位，我们认为 $k3$ 存在于布隆过滤器。实际上 $k3$ 不存在于过滤器，这种发生的概率是 $\frac{1}{n^k}$。
• $hash_{abc}(k3)=(2,~4,~8)$，这些位被置位，我们认为 $k3$ 存在于布隆过滤器。但实际上它的这种情况是 $k1$ 和 $k2$ 组合的结构，也实际不存在，这种情况更容易发生，我们会在后面讨论它发生的概率。
• $hash_{abc}(k3)=(2,~9,~12)$，存在未置位，那么 $k3$ 一定不存在于布隆过滤器。

因此我们发现，通过简单检查哈希序列的置位情况可以判断元素是否存在于集合。如果过滤器认为它存在，可能是误判，这个概率是可配置的，通常是百分之几或千分之几；如果过滤器认为它不存在，则元素一定不存在。

可以发现布隆过滤器基于哈希表的思想，但它与哈希表有两个区别：

• 哈希表通过键值进行检查，冲突时再哈希从而做到冲突的处理。而布隆过滤器不进行冲突处理，将这个工作递交给下层处理。
• 布隆过滤器通过舍弃键值，同时进行位压缩极大节约空间，从而可以表示巨大的磁盘范围。

删除数据

布隆过滤器只能清空重构，无法删除。

例如对于已经创建的布隆过滤器，我们现在希望删除元素 $hash_{abc}(k1)=(1,~2,~8)$，可以发现这里占用的第 $8$ 位是与 $k2$ 共享的，通过布隆计数器我们无法得知是否与其他元素共享某个元素，因此无法删除任一元素。当然这里可以将比特位改成计数，这样就可以实现计数，但例如使用 32 位整数进行计数，就会将内存扩大 32 倍，这与违背了布隆计数器节约空间的初衷。

对于布隆计数器，我们只能清空然后进行重建。

误判率推导

我们现在来详细推导下误判率（False Positive Probability，FPP）的计算。

假设布隆过滤器具有 $n$ 个比特位，$k(k \ll n)$ 次哈希计算，已经进行了 $i$ 次插入。

假设布隆过滤器的 $n$ 个比特位中已经占用了 $x_i$ 个比特位，因为进行 $k$ 次哈希，每次有 $1-\frac{x_i}{n}$ 的概率占用新的比特位。因为 $k \ll n$ 不考虑产生的新比特位产生重叠。

$$\begin{array}{lcl} x_{i+1} & \approx & x_i + k\left(1-\frac{x_i}{n}\right) \\ & = & x_i\left(1-\frac{k}{n}\right) + k & , \\ x_0 & = & 0 \\ \end{array}$$

通过 $x$ 的递推公式，可以求得其通项公式。

$$\begin{array}{rcl} x_{i+1} & = & x_i\left(1-\frac{k}{n}\right) + k \\ x_{i+1} - n & = & x_i\left(1-\frac{k}{n}\right) + k - n \\ \frac{x_{i+1}-n}{x_i-n} & = & 1 - \frac{k}{n} \\ \end{array} \quad\quad \begin{array}{c} \small{\because x_0 = 0} \\ \Longrightarrow \\ \end{array} \quad\quad x_i = n - n\left(1-\frac{k}{n}\right)^i$$

当新的 $k$ 次哈希全部已有的 $x_i$ 个比特位，则认为产生误判，同样这里我们可以因为 $k \ll n$ 近似计算误判率。

$$\begin{array}{lcl} \text{FPP}(i) & = & \frac{\binom{x_i+k-1}{k}}{\binom{n+k-1}{k}} \\ & \approx & \left(\frac{x_i+k-1}{n+k-1}\right)^k \\ & \approx & \left(\frac{x_i}{n}\right)^k \\ & = & \left(1-\left(1-\frac{k}{n}\right)^i\right)^k \\ \end{array} \quad\quad \begin{array}{c} \small{\because k \ll n~~\therefore 1-\frac{k}{n}} \approx e^{-\frac{k}{n}} \\ \Longrightarrow \\ \end{array} \quad\quad \text{FPP}(i) \approx \left(1-e^{-ki/n}\right)^k$$

网上可能有很多版本的推导过程，但是最后进行近似后都得到 $\text{FPP}(i;~n,~k)=\left(1-e^{-ki/n}\right)^k$。

另外可以求得当 $\frac{n}{i}$ 固定且 $k_{best}=(n/i)\ln2$ 时有 $\text{FPP}$ 的最小值。（可见维基百科，我算不来… 但画了图验证）

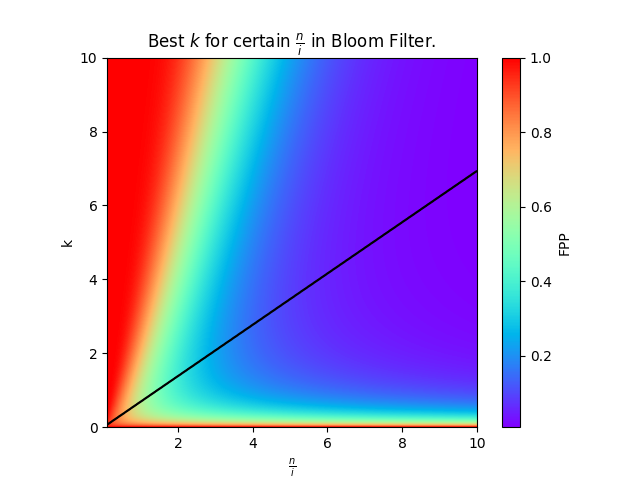
将 $k_{best}$ 代入还可以得到：$\text{FPP} = \left(\frac{1}{2^{\ln2}}\right)^{n/i} \approx 0.6185^{n/i}$。

​因此如果你使用第三方库使用布隆过滤器，通常会传入两个参数： $i$ 表示预计插入元素的次数，$f$ 表示期望达到的误判率。这时库应用上面的推导就可以计算相应的配置：

$$\begin{array}{l} c = \frac{1}{2^{\ln2}}~~~~~~~~~~~~~~~~\approx 0.6185 \\ n = i\cdot\log_{c}{f} \\ k = \ln2\log_{c}{f} \\ \end{array}$$

其中 $n$ 表示推导的布隆过滤器的大小，$k$ 表示需要进行的哈希次数，$c$ 是一个常量。