海明校验码 - 计算机网络

引入：一个有趣的游戏

先丢给大家一个著名的问题：

监狱中甲乙两人密谋越狱，这需要找到逃离监狱的秘密出口。在狱长的房间中有一个国际象棋棋盘，在它 $8 \times 8$ 的棋格上各有一枚硬币，有正有反；同时秘密出口恰好可能出现在监狱的 $64$ 个角落。甲、乙两人事先并不知道棋盘上硬币正反，当然也不知道秘密出口的位置，不过他们在一天晚上商量出了逃离监狱的方案。

第二天甲乙两人分开了。这天早上甲看到了棋盘上所有硬币的正反，同时也知道了钥匙的位置，但他没有机会与乙进行任何交流。甲找到机会偷偷翻动了一枚硬币，然后离开了狱长的房间。下午乙看到了甲留下的棋盘，于是就计算出了秘密出口的位置，并成功逃离。

请问甲乙协商了怎样的方案成功越狱？已知甲乙约定 $8 \times 8$ 的棋格对应恰好 $64$ 个角落；同时约定中甲翻动一枚棋子，约定中甲不可能不翻动棋子。

这个有趣的问题就与我们今天要讲的海明校验码非常相关。我相信你在看完这篇文章后也能解决这个问题，当然你也可以尝试直接解决这个问题，直接解决这个问题可能非常有挑战性。

好吧，跳过这个问题完全不影响对后文海明校验码的理解。🤷‍♂️

什么是海明校验码？

海明校验码（Hamming Code，汉明校验码）是理查德·汉明（Richard W. Hamming）于1950年发明的具有纠错能力的冗余编码。海明校验码可以保证检测 1 或 2 位错误，保证纠错 1 位错误，能检测 3 位及以上的多数错误。

下面我们会讨论海明校验码如何进行编码、解码和纠错、纠错原理。

编码

我们称一段编码中原先具有意义的数据为 消息码，称由海明校验码附加的冗余部分为 冗余码，整个编码则成为 校验码。

海明校验码规定，一段长度为 m 的消息码需要附加长度固定的 r 的冗余码，其中 r 是满足 $2^r \ge m + r + 1$ 的最小正整数解。同时与多数校验码不同，海明校验码中的冗余码不是连续的，它们分别占据校验码的第 $2^i$ 位，其中位是从校验码的低位到高位从 1 开始编号的。

例如 m=11 消息码 11011010101，根据不等式解得 r=4。所以校验码应该为 1101101x010x1xx，其中 x 表示待确定的冗余码，它们分别在第 1,2,4,8 位（再次强调海明校验码中是从 1 开始标位的，不是 0）。下面我们来介绍如何求该冗余码。

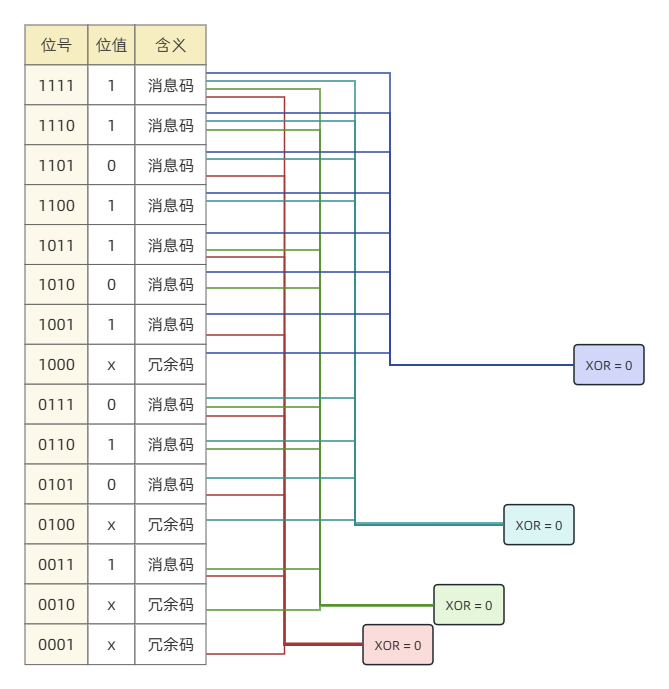
对于 $2^i$ 位冗余码，对所有校验码位 $j$ 该位为 $1$ $\left((2^i~\&~j) \ne 0\right)$ 的组成的集合的异或和应为 $0$ 。例如对于第 $2^0$ 位冗余码，它要求所有位号的最后一位为 $1$ 的位（1,3,5,7,9,11,13,15）的异或和为 $0$ ，解得 $\text{x}_0=0$ ；对于第 $2^2$ 位冗余码，它要求所有位号的第 $2$ 位为 $1$ 的位（4,5,6,7,12,13,14,15）的异或和为 $0$ ，解得 $\text{x}_2=0$ 。

经过上面的操作，可以得到冗余码为 1010，校验码为 110110110100110。我们现在暂且不讨论为什么这么做。

（图中 $\text{x}$ 表示待确定的冗余位）

解码和纠错

解码在没有错误的情况下很简单，在没有错误的情况下，只需舍弃冗余位即可。当然这里的重点是如何进行纠错。

判定没有错误的情况：经过上面的操作，我们保证了所有位号第 $i$ 位为 $1$ 的校验位集合的异或和为 $0$ 。因此如果对于所有 $i$ 满足这个条件，则判定无错，直接舍弃冗余位即可；否则需要进行纠错，然后舍弃冗余位。我们将这个异或和的序列称为错误码，如果错误码全 0 则认为没有错误，否则可以通过纠错码纠错。

下面我们针对几种可能的情况进行说明：

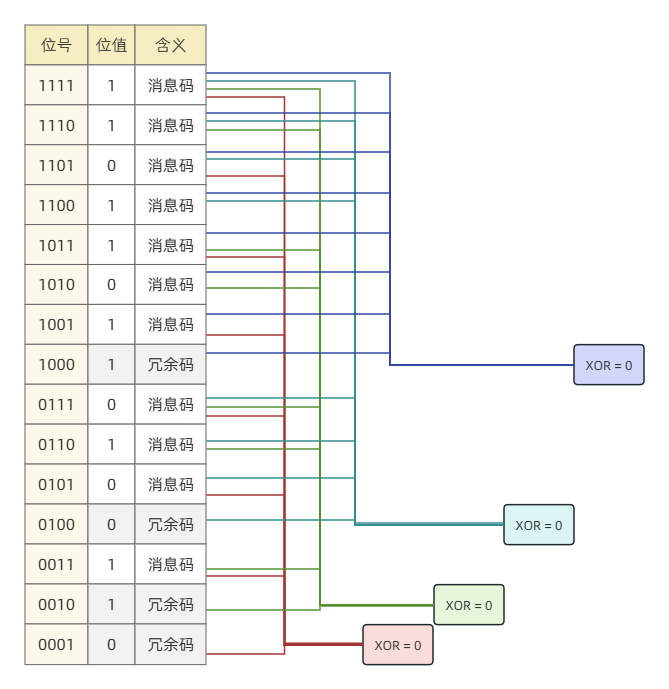
使用和编码一样的计算方式，发现所有异或和都为 $0$ ，因此判定为无错。不需要太多解释，这里确实无错。

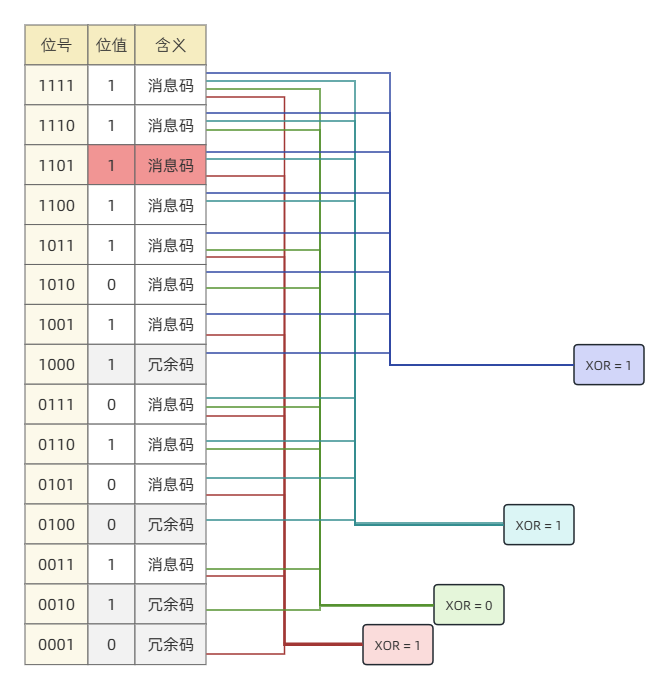
在这个示例中，第 1101 位发生错误，于是导致异或集中引用 1101 的第 3,2,0 位冗余校验发生错误。这个数字正好组成 1101，因此冗余校验产生的错误编码即为发生错误的位。当冗余校验为 0000 时表示没有错误，这也是我们位号必须从 1 开始标位。

另外，不仅是消息码错误可以检测，冗余码也有可能发生错误，同样可以被检测。

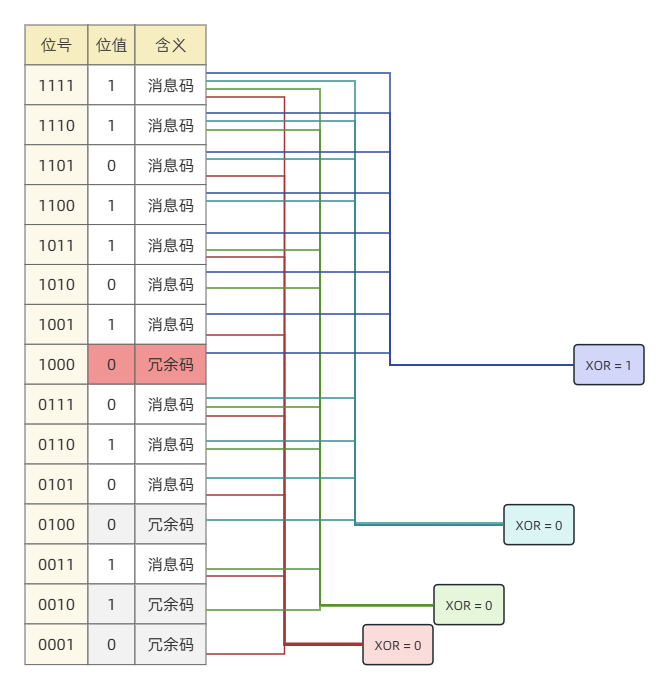
（图中红色表示发生错误的位）

前面两种都是正确纠错的情况，后面介绍可能错误的情况。

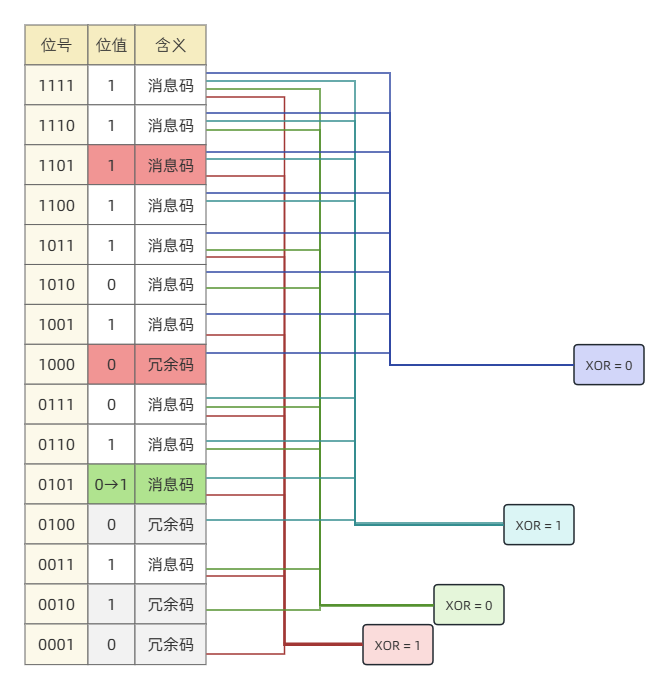
这种情况，你会发现由于发生了多于一处错误，虽然海明校验码检测到了错误，但是由于错误码是两个错误状态的叠加，我们使用错误码的思路索引到了原本正确的位 0101，并反而增加了一处错误。

嗯，但起码检测到了错误。

（图中红色表示发生错误的位，绿色表示被错误纠正的位）

当发生三个错误时，有可能产生判定无错，但实际有错的情况。这里要说明所有发生两个错误的情况都不可能被判定无错。

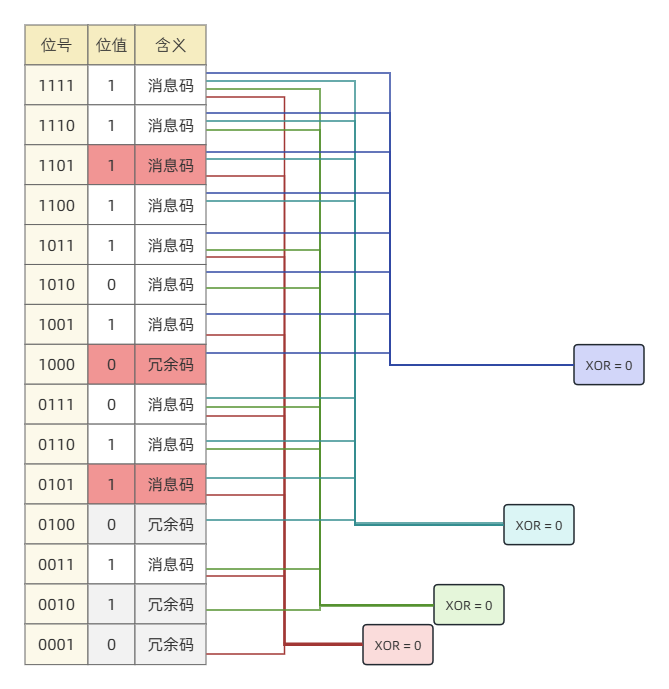
这个案例中，三个错误码 1101、1000、0101 的叠加状态恰好为 0000，被判定为无错。这种情况很难发生，并且一定发生在至少发生三个错误时。

为什么产生两个错误时一定不会发生判定为无错？很容易发现对于任意发生的两个错误，即两个不同的错误码，其异或和一定不为 0，而至少三个错误会导致概率发生异或和为 0。如果一位发生错误的概率为 $p$ ，则产生这种情况的概率 $<p^3$ 。

（图中红色表示发生错误的位）

事实上任何纠错码产生错误纠错的概率永远存在，其作用只能减少发生错误检错的概率。

通过上面的说明，海明校验码有以下特点：保证在发生一个错误时正确纠错，发生两个错误时正确检错但错误纠错，发生三个以上错误时，仍有很大概率成功检错，但无法纠错。

纠错原理（证明）

上面的纠错示例中事实上我们已经在一定程度上介绍了纠错原理，现在我们再进一步梳理一下。

海明校验码在原有的 $m$ 个消息位增加了对数级别 $r$ 个冗余位，从而事实上构建了 $r$ 个集合，通过调节这些冗余位保证 $r$ 个集合内所有位异或和为 $0$ 。一个消息位可以属于多个集合，同时我们还必须保证通过确定是否在每个集合中能够唯一定位一个数据位。例如已知存在一个错误， $\text{x}_3=1$ 就可以得出错误位属于 $\text{x}_3$ 所代表的集合 $S_3$ ， $\text{x}_1=0$ 就可以得出错误位属于 $\text{x}_1$ 所代表的集合 $S_1$ 的补集，通过任意的这样的属于集合或属于补集的描述我们必须都能定位到唯一的数据位。

那么如何建立这套集合体系，使得它们的任意集合-补集描述的交集是唯一的呢？就需要借助二进制这一工具，我们定义所有二进制位号第 $i$ 位为 $1$ 的编码属于集合 $S_i$ 。这时如果我们得知一个数属于集合 $S_i$ 即确定该数位号第 $i$ 位为 $1$ ，如果得知一个数属于集合 $S_i$ 的补集即确定该数位号第 $i$ 位为 $0$ 。这样我们只需要位数个集合就能判定错误的位数。

特别地，上面的体系描述的是存在恰好 1 个错误的情形，但这与实际场景不同。实际场景中，可能出现 0 个（即没有错误）、1 个以及更多个错误。对于 2 个及以上错误我们首先选择弃疗，因为错误个数越多发生的概率是急剧下降的。于是讨论 0 个错误，就有了上面讲到的对于 0 个错误的特殊手段，我们需要空出位号 $0000$ 用于表示没有错误，于是数据位必须从 $1$ 开始编号；换言之，当没有错误时上面的体系正常理解得出了位号 $0000$ 错误的结论，它属于所有集合的补集。至此你可以理解为什么 $r$ 是 $2^r \ge m + r + 1$ 的最小正整数解。

关于 2 个及以上错误的情形，这个体系会得出所有实际错误位的异或和的错误码。海明校验码无法正确理解这种错误，但是我们可以证明当恰好出现两个错误时，它一定不会被判定为无错。